摘要：葛立恒数的平方是否大于原数，这个问题涉及到巨大的数值比较。葛立恒数是一个极其庞大的数，其平方意味着每个位数都要与自己相乘，结果将是一个更为巨大的数。但目前无法确定其平方是否远远大于原数，因为这需要具体的数值计算或证明，远远超出常规数学范畴。

本文目录导读：

1. 葛立恒数的概念及背景
2. 平方数的概念及其增长特性
3. 葛立恒数的平方与葛立恒数本身的比较
4. 相关数学原理及理论支持
5. 拓展思考

当我们谈及葛立恒数时，我们不得不佩服这个数学概念所代表的巨大数值，葛立恒数，由数学天才罗伯特·葛立恒提出，是一个极其庞大的数，其大小远远超出了我们日常生活中的想象，当我们谈论葛立恒数的平方时，是否意味着这个数值远远超过了葛立恒数本身呢？答案是肯定的，本文将详细探讨这一现象背后的数学原理。

葛立恒数的概念及背景

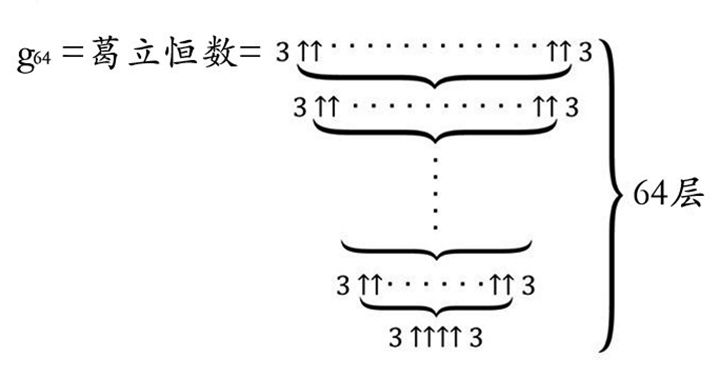
葛立恒数是一个令人难以置信的巨大数值，通常用于描述一些极其庞大的数学问题，它是一个特定的数学问题中的解，这个问题涉及到快速增长的函数和序列，葛立恒数的具体数值是如此之大，以至于我们无法在日常生活中找到与之相对应的实例，它远远超出了我们能够理解的范畴，成为了一个纯粹的数学概念。

平方数的概念及其增长特性

在数学中，一个数的平方意味着该数乘以自身，对于任何正实数来说，其平方都会得到一个远大于原数值的庞大结果，这是因为乘法的性质决定了当我们将一个数乘以自身时，结果会迅速增长，对于已经庞大的葛立恒数来说，其平方无疑将是一个更加巨大的数值。

葛立恒数的平方与葛立恒数本身的比较

为了理解葛立恒数的平方是否远远大于葛立恒数，我们可以从数学的角度进行分析，假设我们有一个正实数N，其平方即为N乘以N，由于乘法具有累加效应，N的平方将是一个远大于N的数值，这一点在葛立恒数上体现得尤为明显，葛立恒数的平方将是葛立恒数本身乘以葛立恒数，结果将是一个极其庞大的数值，远远超过了葛立恒数的原始值。

相关数学原理及理论支持

这种现象背后的数学原理是乘法的性质和快速增长的函数理论，当我们讨论庞大的数值时，乘法的累加效应变得尤为重要，一些特殊的函数，如指数函数，具有快速增长的特性，在这种情况下，一个数的平方可以看作是该数的一个指数函数，当一个已经极其庞大的数值进行平方运算时，结果将以惊人的速度增长。

葛立恒数的平方确实远远大于葛立恒数本身，这一现象背后的数学原理是乘法的性质和快速增长的函数理论，当我们讨论庞大的数值时，这些数学原理变得尤为重要，我们可以得出结论：对于任何庞大的数值来说，其平方都将是一个更加巨大的数值。

拓展思考

这一现象不仅仅局限于葛立恒数，对于任何正实数来说，其平方都会得到一个远大于原数值的庞大结果，这引发我们思考：是否存在更大的数学概念或理论，能够描述这种快速增长的现象？答案可能是肯定的，数学是一门博大精深的学科，其中充满了未知和可能性。

本文探讨了葛立恒数的平方是否远远大于葛立恒数这一问题，通过详细分析乘法的性质、快速增长的函数理论以及相关的数学原理，我们得出结论：对于任何庞大的数值来说，其平方都将是一个更加巨大的数值，这种现象在葛立恒数上体现得尤为明显，我们还探讨了这一现象背后的数学意义以及未来的研究方向。